Joint Entrance Examination (JEE) MAIN will be conducted by the NTA from 2019 onwards. This Examination was being conducted by the Central Board of Secondary Education (CBSE) till 2018.
JEE Main is applicable for admission to NITs, IIITs and CFTIs participating though Central Seat Allocation Board subject to the condition that the candidate should have secured at least 75% marks in the 12th class examination, or be in the top 20 percentile in the 12th class examination conducted by the respective Boards. For SC/ST candidates the qualifying marks would be 65% in the 12thclass examination.
Subject combinations required in the qualifying examination for admission to B.E./B.Tech. & B. Arch./B. Planning Courses in NITs, IIITs, and other CFTIs is as under:-
Course Required Criteria based on Class 12th/ Equivalent qualifying Examination
B.E./B.TECH: Passed qualifying examination with Physics and Mathematics as compulsory subjects along with one of the Chemistry/Biotechnology/Biology Technical Vocational subject.
B.ARCH : Passed qualifying examination with Mathematics, Physics, Chemistry.
B.PLANNING : Passed qualifying examination with Mathematics
The above mentioned policy could also be adopted by other Technical Institutions participating in counselling through JoSAA/CSAB. In case a State opts to admit students in the engineering Colleges affiliated to State Universities, the State may prepare separate rank list based on criteria decided by them.
COURSE STRUCTURE:
Subject Total No. of Question Marks
Physics 25 question 100
Chemistry 25 Question 100
Maths 25 Question 100
Mathematics
UNIT 1: SETS, RELATIONS, AND FUNCTIONS:
Sets and their representation: Union, intersection, and complement of sets and their algebraic properties; Power set; Relation, Type of relations, equivalence relations, functions; one-one, into and onto functions, the composition of functions.
UNIT 2: COMPLEX NUMBERS AND QUADRATIC EQUATIONS:
Complex numbers as ordered pairs of reals, Representation of complex numbers in the form a + ib and their representation in a plane, Argand diagram, algebra of complex number, modulus, and argument (or amplitude) of a complex number, Quadratic equations in real and complex
number system and their solutions Relations between roots and co-efficient, nature of roots, the formation of quadratic equations with given roots.
UNIT 3: MATRICES AND DETERMINANTS:
Matrices, algebra of matrices, type of matrices, determinants, and matrices of order two and three, evaluation of determinants, area of triangles using determinants, Adjoint, and evaluation of inverse of a square matrix using determinants and, Test of consistency and solution of simultaneous linear equations in two or three variables using matrices.
UNIT 4: PERMUTATIONS AND COMBINATIONS:
The fundamental principle of counting, permutation as an arrangement and combination as section, Meaning of P (n,r) and C (n,r), simple applications.
UNIT 5: BINOMIAL THEOREM AND ITS SIMPLE APPLICATIONS:
Binomial theorem for a positive integral index, general term and middle term, and simple applications.
UNIT 6: SEQUENCE AND SERIES:
Arithmetic and Geometric progressions, insertion of arithmetic, geometric means between two given numbers, Relation between A.M and G.M.
UNIT 7: LIMIT, CONTINUITY, AND DIFFERENTIABILITY:
Real–valued functions, algebra of functions, polynomials, rational, trigonometric, logarithmic, and exponential functions, inverse function. Graphs of simple functions. Limits, continuity, and differentiability. Differentiation of the sum, difference, product, and quotient of two functions. Differentiation of trigonometric, inverse trigonometric, logarithmic, exponential, composite, and implicit functions; derivatives of order up to two, Applications of derivatives:
Rate of change of quantities, monotonic-Increasing and decreasing functions, Maxima and minima of functions of one variable.
UNIT 8: INTEGRAL CALCULAS:
Integral as an anti-derivative, Fundamental integral involving algebraic, trigonometric, exponential, and logarithmic functions. Integrations by substitution, by parts, and by partial functions. Integration using trigonometric identities.
Evaluation of simple integrals of the type
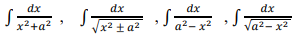
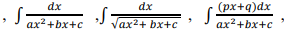
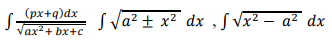
The fundamental theorem of calculus, properties of definite integrals. Evaluation of definite integrals, determining areas of the regions bounded by simple curves in standard form.
UNIT 9: DIFFRENTIAL EQUATIONS
Ordinary differential equations, their order, and degree, the solution of differential equation by the method of separation of variables, solution of a homogeneous and linear differential equation of the type
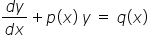
UNIT 10: CO-ORDINATE GEOMETRY
Cartesian system of rectangular coordinates in a plane, distance formula, sections formula, ocus, and its equation, the slope of a line, parallel and perpendicular lines, intercepts of a line on the co-ordinate axis.
Straight line
Various forms of equations of a line, intersection of lines, angles between two lines, conditions for concurrence of three lines, the distance of a point form a line, co-ordinate of the centroid, orthocentre, and circumcentre of a triangle,
Circle, conic sections
A standard form of equations of a circle, the general form of the equation of a circle, its radius and central, equation of a circle when the endpoints of a diameter are given, points of intersection of a line and a circle with the centre at the origin and sections of conics, equations of conic sections (parabola, ellipse, and hyperbola) in standard forms.
UNIT 11: THREE DIMENSIONAL GEOMETRY
Coordinates of a point in space, the distance between two points, section formula, directions ratios, and direction cosines, and the angle between two intersecting lines. Skew lines, the shortest distance between them, and its equation. Equations of a line
UNIT 12: VECTOR ALGEBRA
Vectors and scalars, the addition of vectors, components of a vector in two dimensions and three-dimensional space, scalar and vector products.
UNIT 13: STATISTICS AND PROBABILITY
Measures of discretion; calculation of mean, median, mode of grouped and ungrouped data calculation of standard deviation, variance, and mean deviation for grouped and ungrouped data.
Probability: Probability of an event, addition and multiplication theorems of probability, Baye's theorem, probability distribution of a random variate.
UNIT 14: TRIGONOMETRY
Trigonometrical identities and trigonometrical functions, inverse trigonometrical functions, and their properties.