The Syllabus in the subject of Mathematics has undergone changes from time to time in accordance with growth of the subject and emerging needs of the society. The present revised syllabus has been designed in accordance with National Curriculum Framework 2005 and as per guidelines given in the Focus Group on Teaching of Mathematics which is to meet the emerging needs of all categories of students. For motivating the teacher to relate the topics to real life problems and other subject areas, greater emphasis has been laid on applications of various concepts.
The curriculum at Secondary stage primarily aims at enhancing the capacity of students to employ Mathematics in solving day-to-day life problems and studying the subject as a separate discipline. It is expected that students should acquire the ability to solve problems using algebraic methods and apply the knowledge of simple trigonometry to solve problems of height and distances. Carrying out experiments with numbers and forms of geometry, framing hypothesis and verifying these with further observations form inherent part of Mathematics learning at this stage. The proposed curriculum includes the study of number system, algebra, geometry, trigonometry, mensuration, statistics, graphs and coordinate geometry, etc.
The teaching of Mathematics should be imparted through activities which may involve the use of concrete materials, models, patterns, charts, pictures, posters, games, puzzles and experiments.
Objectives
The broad objectives of teaching of Mathematics at secondary stage are to help the learners to:
- consolidate the Mathematical knowledge and skills acquired at the upper primary stage;
- acquire knowledge and understanding, particularly by way of motivation and visualization, of basic concepts, terms, principles and symbols and underlying processes and skills;
- develop mastery of basic algebraic skills;
- develop drawing skills;
- feel the flow of reason while proving a result or solving a problem;
- apply the knowledge and skills acquired to solve problems and wherever possible, by more than one method;
- to develop ability to think, analyze and articulate logically;
- to develop awareness of the need for national integration, protection of environment, observance of small family norms, removal of social barriers, elimination of gender biases;
- to develop necessary skills to work with modern technological devices and mathematical software's.
- to develop interest in mathematics as a problem-solving tool in various fields for its beautiful structures and patterns, etc.
- to develop reverence and respect towards great Mathematicians for their contributions to the field of Mathematics;
- to develop interest in the subject by participating in related competitions;
- to acquaint students with different aspects of Mathematics used in daily life;
- to develop an interest in students to study Mathematics as a discipline.
COURSE STRUCTURE CLASS -X
Units Unit Name Marks
I Number System 06
II Algebra 20
III Coordinate Geometry 06
IV Geometry 15
V Trignometry 12
VI Mensuration 10
VII Statistics & Probability 11
Total 80
UNIT I: NUMBER SYSTEMS
1. REAL NUMBER
Euclid’s division lemma, Fundamental Theorem of Arithmetic - statements after reviewing work done earlier and after illustrating and motivating through examples, Proofs of irrationality of
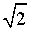
,
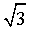
,
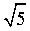
Decimal representation of rational numbers interms of terminating/non-terminating recurring decimals.
UNIT II: ALGEBRA
1. POLYNOMIALS
Zeros of a polynomial. Relationship between zeros and coefficients of quadratic polynomials. Statement and simple problems on division algorithm for polynomials with real coefficients.
2. PAIR OF LINEAR EQUATIONS IN TWO VARIABLES
Pair of linear equations in two variables and graphical method of their solution, consistency/inconsistency.
Algebraic conditions for number of solutions. Solution of a pair of linear equations in two variables algebraically - by substitution, by elimination and by cross multiplication method. Simple situational problems. Simple problems on equations reducible to linear equations.
3. QUADRATIC EQUATIONS
Standard form of a quadratic equation ax2 + bx + c = 0, (a ≠ 0). Solutions of quadratic equations (only real roots) by factorization, and by using quadratic formula. Relationship between discriminant and nature of roots.
Situational problems based on quadratic equations related to day to day activities to be incorporated.
4. ARITHMETIC PROGRESSIONS
Motivation for studying Arithmetic Progression Derivation of the nth term and sum of the first n terms of A.P. and their application in solving daily life problems.
UNIT III: COORDINATE GEOMETRY
Coordinate Geometry
Review: Concepts of coordinate geometry, graphs of linear equations. Distance formula. Section formula (internal division).
UNIT IV: GEOMETRY
1. TRIANGLES
Definitions, examples, counter examples of similar triangles.
1. (Prove) If a line is drawn parallel to one side of a triangle to intersect the other two
sides in distinct points, the other two sides are divided in the same ratio.
2. (Motivate) If a line divides two sides of a triangle in the same ratio, the line is parallel
to the third side.
3. (Motivate) If in two triangles, the corresponding angles are equal, their corresponding
sides are proportional and the triangles are similar.
4. (Motivate) If the corresponding sides of two triangles are proportional, their
corresponding angles are equal and the two triangles are similar.
5. (Motivate) If one angle of a triangle is equal to one angle of another triangle and the
sides including these angles are proportional, the two triangles are similar.
2. CIRCLES
Tangent to a circle at, point of contact
1. (Prove) The tangent at any point of a circle is perpendicular to the radius through the
point of contact.
2. (Prove) The lengths of tangents drawn from an external point to a circle are equal.
UNIT V: TRIGONOMETRY
1. INTRODUCTION TO TRIGONOMETRY
Trigonometric ratios of an acute angle of a right-angled triangle. Proof of their
existence (well defined); motivate the ratios whichever are defined at 0o and 90o. Values
of the trigonometric ratios of 300
, 450
and 600
. Relationships between the ratios.
2. TRIGONOMETRIC IDENTITIES
Proof and applications of the identity sin2A + cos2A = 1. Only simple identities to be
given.
3. HEIGHTS AND DISTANCES: Angle of elevation, Angle of Depression.
Simple problems on heights and distances. Problems should not involve more than two
right triangles. Angles of elevation / depression should be only 30°, 45°, and 60°.
UNIT VI: MENSURATION
1. AREAS RELATED TO CIRCLES
Area of sectors and segments of a circle. Problems based on areas and perimeter /
circumference of the above said plane figures. (In calculating area of segment of a
circle, problems should be restricted to central angle of 60°, 90° and 120° only.
2. SURFACE AREAS AND VOLUMES
Surface areas and volumes of combinations of any two of the following: cubes, cuboids, spheres, hemispheres and right circular cylinders/cones.
UNIT VII: STATISTICS AND PROBABILITY
1. STATISTICS
Mean, median and mode of grouped data (bimodal situation to be avoided).
2. PROBABILITY
Classical definition of probability. Simple problems on finding the probability of an event.